백준 15902번 문제 Split and Merge는 UCPC 2018의 예선대회 문제로, 작년에 우리 팀이 UCPC 2019를 준비하는 과정에서 연습삼아 본 문제 중 하나이다. 팀연습 시간에 풀어내지 못한, solved.ac 기준 다이아 5의 난이도를 가진 어려운 문제이다.
결국 나는 이 문제를 새벽 내내 붙잡아 풀어냈었다.
문제는 내가 왜 맞는지 알 수 없는 방법으로 문제를 해결했다는 것이다. 그래서 당시에 1. 내가 문제를 푼 방법을 기록하고자, 또 2. 그 방법이 왜 작동하는지를 증명하고자 하였으나, 계속 미루다가 결국 1년이 지난 오늘에서야 코드를 다시 열어본다.
그래서 지금 작년의 내가 짠 코드를 보고 있는데, 이를 해석하려면 조금 시간이 걸릴 것 같다...
드디어 코드 해석을 마쳤다.
작년에 내가 문제를 풀면서 거친 사고의 과정을 그대로 밟아보겠다.
편의를 위해 초기 상태를 $a$, 최종 상태를 $b$라고 부르자.
$a$와 $b$에 동시에 존재하는 구분선을 기준으로 문제를 쪼갤 수 있다
$a$와 $b$에 동시에 존재하는 구분선은 연산을 행하는 도중에 없앨 이유가 없으므로, 이러한 '겹치는 구분선'을 기준으로 격자를 나누어 문제를 풀면 된다. 이렇게 나눠진 격자들을 각각 'segment'라고 부르자.
각 segment마다 필요한 연산의 수와, 가능한 연산 순서의 경우의 수를 각각 구했다고 가정하자.
그러면 문제가 어렵지 않게 풀린다.
총 연산의 수는 단순히 각 segment에서 필요한 연산의 수의 총합으로 구하면 된다.
총 경우의 수는 조금 더 복잡하다. 전체 연산중에서 1. 어떤 연산을 어떤 segment를 위한 연산으로 사용할지를 먼저 할당한 후, 2. 각 segment의 연산 순서 경우의 수를 곱해주면 된다. 1번의 경우의 수는 중복이 있는 수열의 배치 경우의 수를 생각하면 된다. 이해를 위해 예시를 들겠다. Segment가 3개 있고, 각각에서 필요한 연산의 수가 $x$, $y$, $z$이고 각각에서 연산을 배열할 수 있는 순서의 개수가 $X$, $Y$, $Z$라고 하자. 그렇다면 총 경우의 수는 $\frac {(x + y + z)!}{x!y!z!} \times X \times Y \times Z$가 될 것이다.
고로 이제 우리의 목표는 각 segment에 대해 문제를 푸는 것이다.
Segment의 모양은 (거의) 항상 규칙적이다
'겹치는 구분선'을 기준으로 나눠진 격자인 segment는 항상 $a$와 $b$의 구분선이 교차하는 형태일 수밖에 없다. 아래 그림을 참고하면 이해가 쉬울 것이다.

주황색으로 표시된 segment는 구분선이 교차하는 형태가 아닌 유일한 segment이다. 이 segment는 연산이 필요하지도 않으므로, 예외로 처리하도록 하겠다. 이제는 예외가 아닌 segment들을 살펴보자.
양 끝을 제외한, 모든 구분선이 존재할 수 있는 위치에 대해서 split 또는 merge 연산이 한번 수행되어야 한다. 고로 segment당 총 연산의 수는 segment의 길이에서 1을 뺀 값이다. 이제 (길이) - 1개의 연산의 가능한 실행 순서는 몇 가지가 될지 살피기만 하면 된다.
Merge 연산을 위해서는 양쪽에 구분선이 이미 존재해야 한다
Merge 연산을 위해서는 merge를 통해 합해지는 두 칸의 바깥쪽 끝에 구분선이 존재해야 한다. 이것이 연산의 순서에 있어서 유일한 제약이다. 경우의 수를 어떻게 구할지 한참을 고민하다가, 전탐색을 통해서 규칙성을 파악해 보기로 하였다. 다음은 segment의 길이 n이 1부터 9일 때까지 연산 순서 배치의 경우의 수를 계산해주는 [Python 스크립트]의 실행 결과이다.
1 1
2 1
3 2
4 5
5 16
6 61
7 272
8 1385
9 7936$1, 1, 2, 5, 16, 61, 272, 1385, 7936$을 검색해 보았더니 월척이다. OEIS의 A000111 수열인 Euler number이다.
Euler Number는 무엇이고, 계산은 어떻게 하지?
Euler Number는 길이 $n$짜리 alternating permutation의 개수의 수열이다. (정확히 말하자면 지금 구하고자 하는 A000111 수열은 alternating permutation의 개수의 절반인 Euler up/down numbers 혹은 Euler zigzag numbers이다. Alternating permutation이란 1, 3, 2, 4처럼 커지고 작아지기를 반복하거나 4, 2, 3, 1처럼 작아지고 커지기를 반복하는 permutation을 뜻하며, Euler up/down numbers는 [커지고 작아지는 수열]과 [작아지고 커지는 수열] 중 하나만 센 것이다.)
이는 또 다른 수열인 Entringer Number를 통해 계산할 수 있다고 한다.
Entringer Number $E(n, k)$는 길이가 $n$이고 $k$로 시작하는 alternating permutation의 개수이다. 고로 Euler Number $A_n$은 $\sum_{k=1}^{n} E(n, k)$로 구해진다. 그런데 Entringer Number는 다음과 같은 점화식이 있다고 한다:
$$E(0, 0) = 1, E(n, 0) = 0$$
$$E(n, k) = E(n, k - 1) + E(n - 1, n - k)$$
문제가 풀리는 순간이다.
구현은 [이렇게] 했다.
여기까지가 작년에 내가 풀어낸 내용이다.
이제 남은 질문은 왜 이 문제가 alternating permutation으로 풀리는지이다...
고민 끝에 이 또한 해결하였다.
점화식을 통한 증명
먼저 이 문제의 정해를 참고하였다.
정해 또한 DP 풀이인데, $a$에서 $b$로 바꾸기 위한 첫 연산은 항상 split 연산임에 주목하여 문제를 더 작은 문제로 회귀시킨다. 이미지로 확인하자.
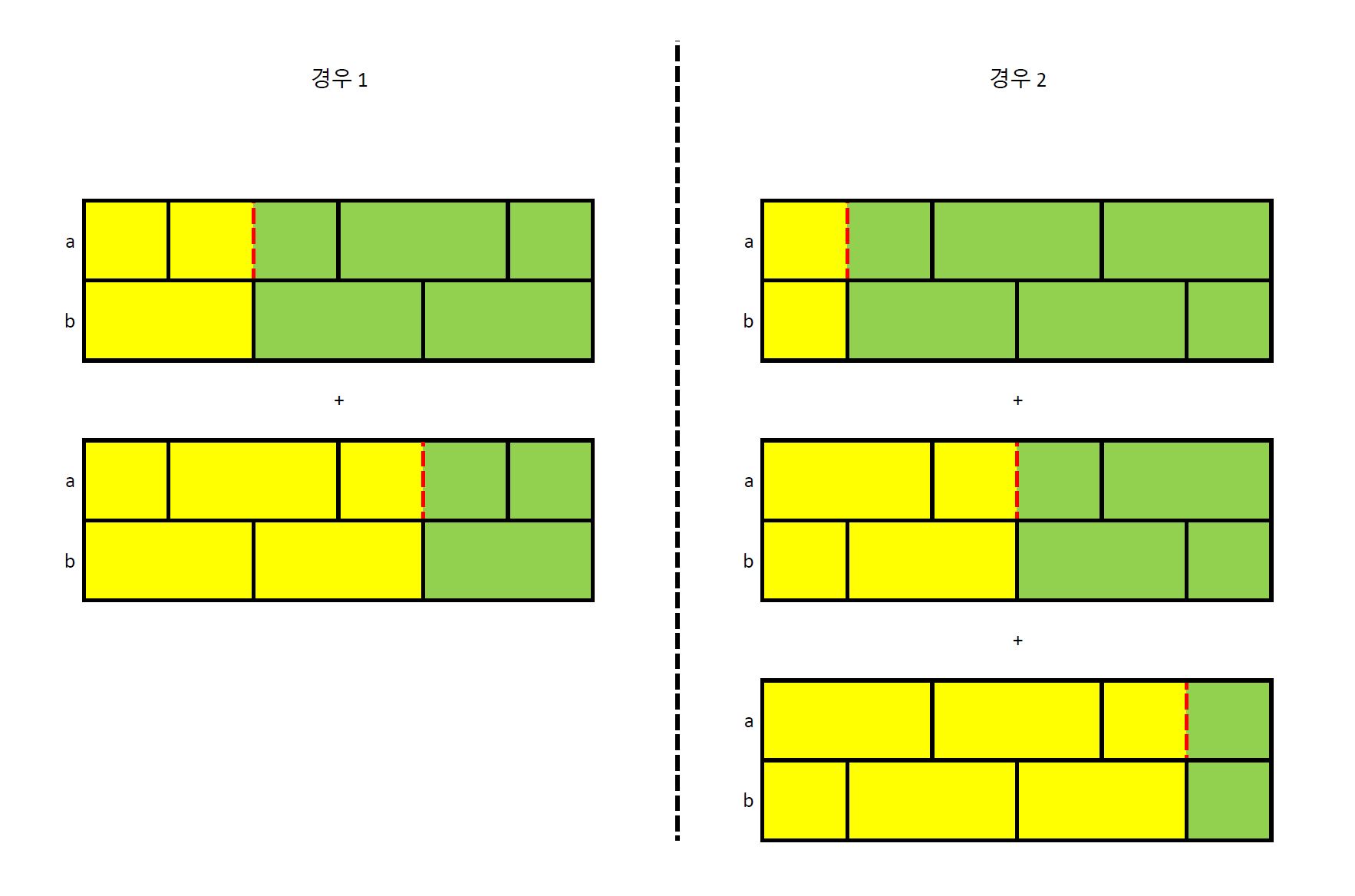
길이 6짜리 segment를 예시로 들자면, 위의 이미지에서 확인 가능하듯이 경우 1과 경우 2의 두 가지가 있다. 우선 경우 1과 2는 총 가능한 연산의 순서의 개수가 같다(왜냐면 경우 1에서 거친 연산을 그대로 거꾸로 밟으면 경우 2의 솔루션에 일대일 대응되기 때문이다).
빨간 점선은 첫 연산으로 택한 split 지점이다. Split 연산 이후에 segment가 더 작은 segment 두개로 나누어짐을 확인할 수 있다. 고로 원래 segment에서 가능한 연산의 순서는, 쪼개진 두개의 segment에서 각각 가능한 연산의 순서의 개수의 곱에다가 그 두 segment 연산의 순서를 배정하는 경우의 수를 추가로 곱해줘서 구할 수 있다. 따라서 경우 1의 경우, 총 연산 순서의 경우의 수는
$$A_6 = \binom {4}{1} A_2 A_4 + \binom {4}{3} A_4 A_2$$
이다. 동시에 경우 2로부터
$$A_6 = \binom {4}{0} A_1 A_5 + \binom {4}{2} A_3 A_3 + \binom {4}{4} A_5 A_1$$
이다. 고로 이 둘을 합하면
$$2A_6 = \binom {4}{0} A_1 A_5 + \binom {4}{1} A_2 A_4 + \binom {4}{2} A_3 A_3 + \binom {4}{3} A_4 A_2 + \binom {4}{4} A_5 A_1$$
이고, 이를 일반화하면
$$2A_{n+1} = \sum_{k=1}^{n} {\binom {n - 1}{k - 1} A_k A_{n - k + 1}}$$
임을 확인할 수 있다. 현재 우리는 $A$수열의 시작 인덱스를 1로 두고 있는데, 비교를 위해 우리 또한 인덱스를 0부터 시작하도록 바꾼 후 방금의 식을 다시 정리해보면
$$2A_{n+1} = \sum_{k=0}^{n} {\binom {n}{k} A_k A_{n - k}}$$
라는 아주 예쁜 식이 나온다. 그런데 이 식이 위키피디아의 alternating permutation 페이지의 André's theorem 항목 아래에 그대로 있다.
점화식과 초기값이 일치하므로, 우리가 구하려는 경우의 수는 alternating permutation의 개수인 Euler Number가 된다.
증명 끝...
...이긴 하지만 조금 더 직관적인 이유를 원한다. 도대체 이 문제에서 alternating permutation이 어떻게 도출될까?
일대일 대응을 통한 증명
조금 더 직관적인 증명을 위해, 길이 $n$짜리 segment의 연산 순서와 길이 $n - 1$짜리 alternating permutation 사이의 일대일 대응을 보이고 싶었다.
숨어있던 일대일 대응을 발견하도록 도와준 것은 작년에 작성했던 전탐색 코드이다. 먼저 나의 전탐색 코드를 설명한다:
{
한 segment를 $a$에서 $b$로 바꾸기 위해서는, 모든 칸의 경계에 대해 한번씩의 연산이 필요하다. 만약 그 경계가 이미 쪼개져 있었다면 merge 연산, 합해져 있었다면 split 연산을 한번씩 해야하기 때문이다. 고로 모든 연산에 번호를 붙일 수가 있다. 첫번째 경계에 대한 연산은 1번 연산, 두번째 경계에 대한 연산은 2번 연산, 세번째 경계에 대한 연산은 3번 연산... 이런식으로 말이다. 아래 그림 참고.

그럼 이제 [연산의 순서]와 [permutation]을 일대일 대응시킬 수 있다. 예를 들어 2번과 4번 위치에서 split을 수행한 후 1번, 3번, 5번을 merge하는 연산 순서는 {2, 4, 1, 3, 5}에 대응한다. 길이 6짜리 segment에서 가능한 연산의 순서의 개수는 길이 5짜리 permutation 중 홀수 번호 연산이 인접한 짝수 번호 연산보다 늦게 배치되어있는 permutation의 개수와 일치한다. 1번 merge 연산보다 2번 split 연산이 먼저 있어야 하고, 이는 다른 위치에서도 마찬가지이기 때문이다.
그래서 내 전탐색 코드는 단순히 길이 $n - 1$짜리 permutation 중에서 모든 홀수 번호가 인접한 짝수 번호보다 늦게 나오는 것들의 개수를 세어주었다. (여기서 홀짝성을 바꿔서 생각해도 상관 없다. 앞 그림의 [경우 1]과 [경우 2]의 차이일 뿐이다.)
}
이 전탐색 방식에서 나는 alternating permutation과의 공통점 하나를 느꼈다. 일단 alternating permutation 중 [작아지고 커지는 수열]과 대응시켜보자(e.g. 4, 1, 3, 2).
- 작아지고 커지는 alternating permutation의 홀수 번째 숫자는 그 양옆 숫자들보다 커야 한다.
- 우리의 문제에서 segment 안의 홀수 번째 연산은 그 양옆 연산보다 뒤에 배치되어야 한다.
전혀 상관 없어보이던 두 문제 사이의 연관성이 보이는 순간이다. 우리의 문제의 경우, 연산 순서를 나타낸 permutation에서 홀수는 그 크기상 위아래의 짝수보다 위치상 뒤에 있어야 한다. Alternating permutation의 경우, 위치상 홀수 번째 숫자는 그 양옆 숫자들보다 크기상 커야 한다. 위치와 크기의 완벽한 대칭이다.
이러한 통찰을 바탕으로, 이제 두 문제를 일대일 대응시킬 수 있다. 앞서 예시로 든 연산 순서 {2, 4, 1, 3, 5}를 대응하는 alternating permutation으로 바꿔보자. 2는 1보다 두 위치 앞에 있다. 3은 2보다 세 위치 뒤에 있다. 4는 3보다 두 위치 앞에 있다. 5는 4보다 세 위치 뒤에 있다. 위치를 크기로, 값을 위치로 바꾸자. 두 번째 값은 첫 번째 값보다 2 작다. 세 번째 값은 두 번째 값보다 3 크다. 네 번째 값은 세 번째 값보다 2 작다. 다섯 번째 값은 네 번째 값보다 3 크다. 결과는 {3, 1, 4, 2, 5}가 된다.
이쯤 되면 충분한 설명인 것 같다.
출제진들도 이 문제와 alternating permutation 사이의 관계는 모르겠지 ㅋㅋ
-끝-
아 해결했다 ㅎㅎ
1년동안 거슬리던 문제를 기분 좋게 치운 날이다.
솔직히 작년에 이 문제를 OEIS를 통해 해결했을 때만 해도, 왜 이 풀이가 되는지를 정말로 내가 찾아내리라고는 상상도 못했다. 요즘 계속 할일만 쌓이는 나인데, 하나를 완벽히 정리할 수 있어서 다행이다.
이젠 내일 UCPC 2020이나 열심히 해야지..!