자다 일어나자마자 Nyso의 연락을 받고 대회 레지스터.
초반 문제를 최대한 빨리 풀겠다는 마음으로 임했다.
A: Suborrays
그냥 아무거나 출력하면 된다.
2분에 AC
B: Fix You
젤 오른쪽 column과 젤 아래 row만 살피면 된다.
5분에 AC
Cycle이 생기는 조건을 먼저 찾아내고자 했다. 잘 생각해보니 permutation의 값들이 내려갔다가 올라가는 경우, 즉 $2, 1, 3$과 같은 배치인 경우 cycle이 생긴다. 이 두 조건이 동치인 것을 증명하기 전에 그냥 구현하고 제출해보기로 했다.
경우의 수를 세는 방법은 두가지가 있다. 직접 세주는 방법과 여집합을 이용한 방법이다. 여집합을 이용하는 경우, 값들이 올라가서 고점을 찍고 내려가는 경우를 세준 후, 전체 경우의 수에서 빼주면 된다. 나는 반대로 직접 세주었다. 길이 $n$짜리 permutation에서, $1$이 중간에 위치한다면 무조건 내려갔다가 올라가는 지점이 존재한다. 만약 $1$이 중간이 아닌 양 끝 중 하나에 위치한다면, 길이 $n - 1$짜리 permutation에 대한 문제가 된다. 고로 $A_n = (n - 2) \cdot (n - 1)! + 2 \cdot A_{n - 1}$이다. (여집합으로 계산한다면 $O(1)$ 복잡도도 가능하다.)
27분에 AC
D: 505
구데기 문제.
4x4 크기 이상부터는 불가능하므로, 한 변이 1, 2, 3인 경우로 나눠서 풀면 된다.
1인 경우, 아무것도 바꾸지 않아도 된다.
2인 경우, 2x2 행렬들을 전부 다 합이 홀수로 만들어주기 위해서는, 세로줄의 합이 번갈아가며 홀수와 짝수이어야 한다. 홀짝홀짝으로 만들지, 아니면 짝홀짝홀로 만들지는 두 경우 다 해보고 비교해보면 된다.
3인 경우, 2인 경우 두개가 한 row를 끼고 겹쳐있는 상황으로 이해할 수 있다. 윗쪽 줄과 아랫쪽 줄의 목표 홀짝 상태를 결정한 이후, 위와 아래에서 모두 변경이 필요한 세로줄의 경우, 가운데 row의 값 하나만을 변경해서 한 번의 operation을 줄일 수 있다. 그냥 윗줄 목표상태 2가지, 아랫줄 목표상태 2가지를 곱해서 총 4가지 경우를 다 살펴보도록 구현하였다.
정해는 DP인 듯 하나, DP를 떠올리기도 전에 위의 풀이가 먼저 생각나는 간단한 문제이다. 하지만 이걸 구현하자니 너무 구데기스러웠다. 오타찾기를 25분간 했다.
1시간 23분에 AC
총평
D번이 이상하다...
D를 풀고, 레이팅 방어 상태로 만들어둔 후 빠르게 대회와 손절했다. 앞 문제들을 빠르게 해결해서 다행이다.
레이팅 변화 1911 + 24 = 1935
My Performance: ★★★☆☆
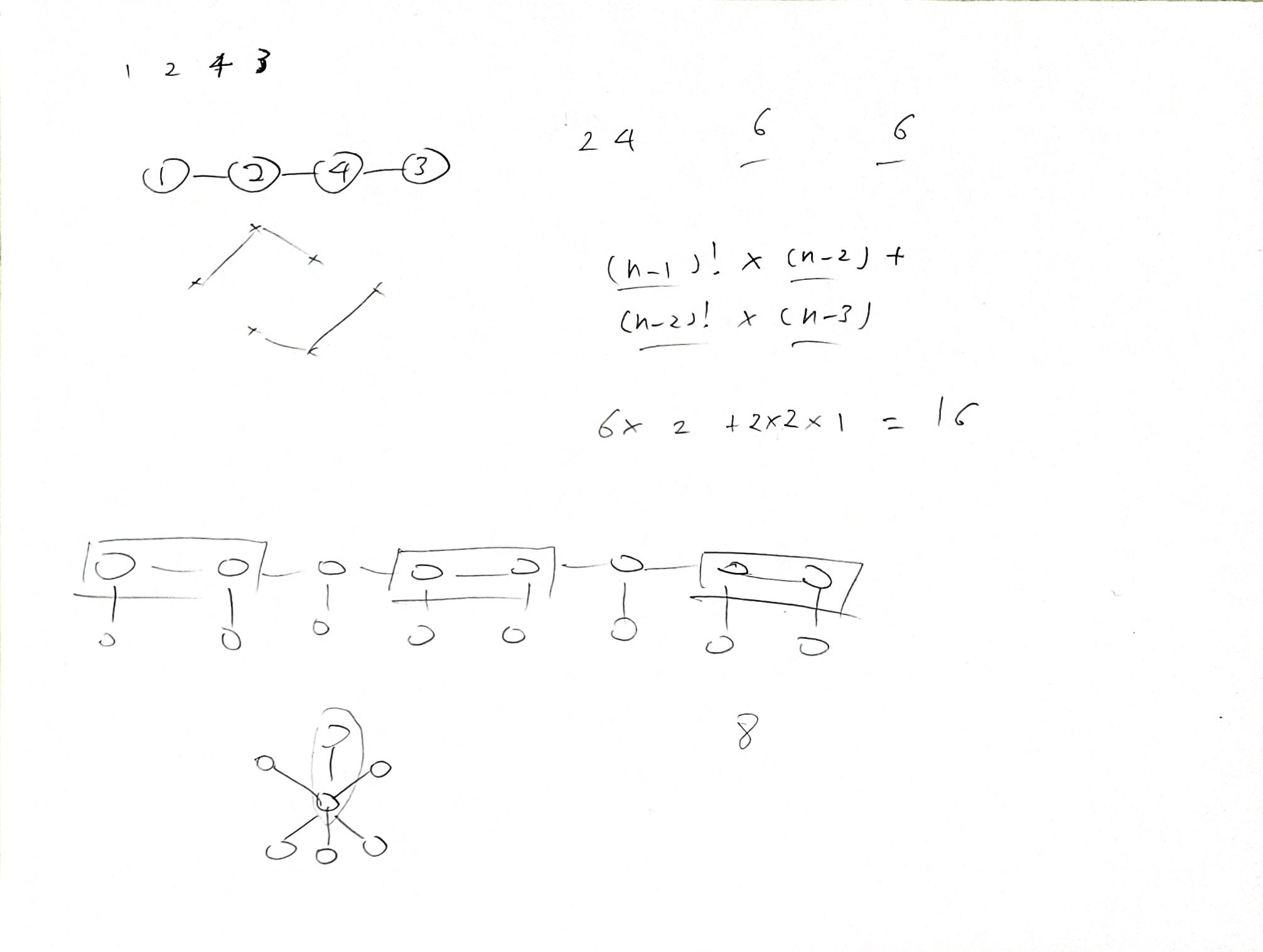
연습지
'Competitive Programming > Codeforces' 카테고리의 다른 글
| 대회후기: Educational Codeforces Round 101 (Rated for Div. 2) (0) | 2020.12.30 |
|---|---|
| 대회후기: Codeforces Round #678 (Div. 2) (0) | 2020.10.26 |
| 대회후기: Codeforces Round #662 (Div. 2) (0) | 2020.08.10 |
| 대회후기: Codeforces Round #658 (Div. 2) (2) | 2020.07.24 |
| 대회후기: Codeforces Global Round 9 (3) | 2020.07.05 |